

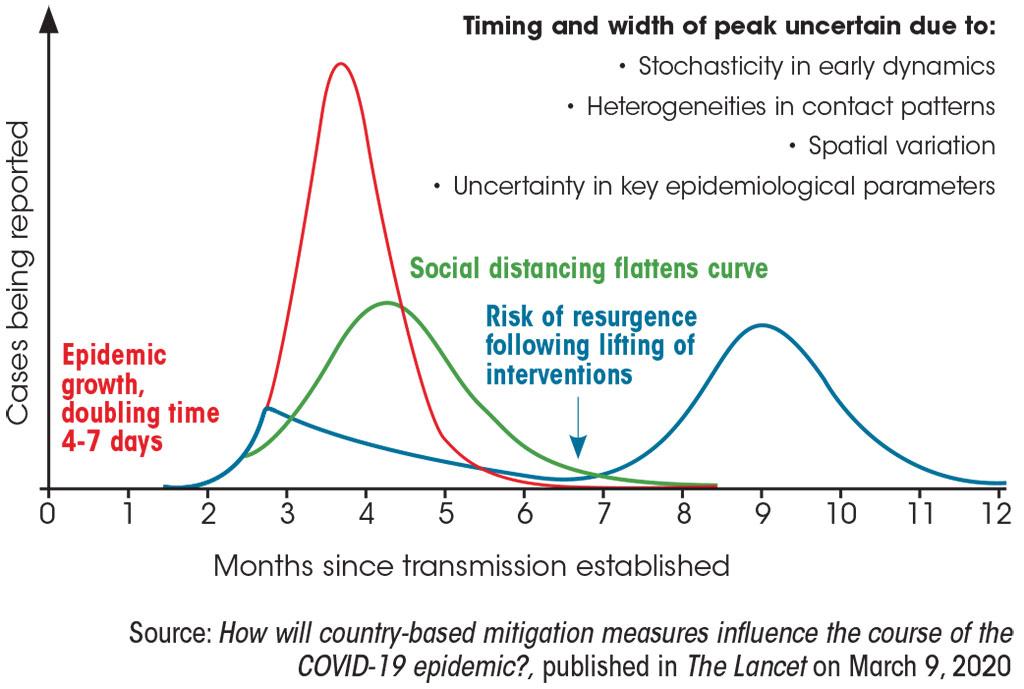
Projected paths of the pandemic



Exponential curve This offers the worst case scenario, where the virus spreads uncontrollably. Since the word “exponent” is grounded in algebra, the curve suggests a rapid increase of the infected, as is typical of exponential growth. Let’s take a conservative estimate. If a sick person infects two others in a day, there will be 16,000 cases after 14 days. The infection rate, though varies from country to country, is higher for COVID-19, suggesting a steeper infection curve. During this rapid infection growth phase, the number of people needing hospitalisation can grow in leaps and bounds, overwhelming the local healthcare system. More hospitals may run out of basic supplies they need to respond to the outbreak.
Flatten the curve Since there is no vaccine to medicine to treat COVID-19 and only limited testing kits to diagnose the virus, flattening the curve is the only effective intervention to limit the spread of the virus. The infection rate can be reduced through a combination of collective actions, such as social distancing of the entire population, case isolation, household quarantine and school and university closure. Though the same number of people may get infected in a flatter-curve scenario as in the exponential-curve scenario, a slower infection rate ensures a less stressed healthcare system, fewer hospital visits on any given day and fewer sick people being turned away.
Sine curve This is the basic example of a periodic curve, a graph that keeps repeating. Flattening the curve can help reduce the rate of transmission. But there will still be the risk of resurgence once interventions are relaxed. Interventions like social distancing may thus need to be in place until a vaccine is developed—after 18 months or longer.
We are a voice to you; you have been a support to us. Together we build journalism that is independent, credible and fearless. You can further help us by making a donation. This will mean a lot for our ability to bring you news, perspectives and analysis from the ground so that we can make change together.

Comments are moderated and will be published only after the site moderator’s approval. Please use a genuine email ID and provide your name. Selected comments may also be used in the ‘Letters’ section of the Down To Earth print edition.